プログラマならみんな知ってるよね!データ構造と計算量について

mukku

2013.12.14

システムエンジニア

9日目らくさんの記事を読んで計算量を意識することがいかに重要かということを学んだ、ムックです。

というわけで、ソニックムーブ Advent Calendar 2013 14日目はプログラマならみんな知っているであろう、データ構造と計算量について改めて調べてみました。

まず、データ構造とは

データ構造（データこうぞう、英: data structure）は、計算機科学において、
データの集まりをコンピュータの中で効果的に扱うため、一定の形式に系統立てて格納するときの形式のことである。 — wikipedia抜粋

データ構造には、いくもの種類があるが良し悪しがなくどういったデータをどう処理するかによって効率が大きく変わっていきます。

データ構造の主な種類
まとめ
- ケーステストのソース

データ構造の主な種類

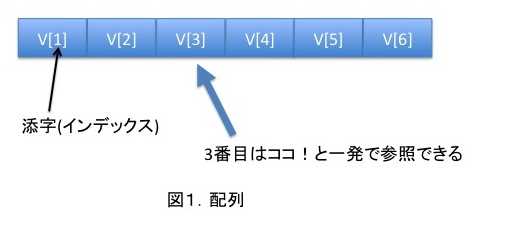
配列(Array)

プログラムをかじったことがある人は誰しも知っているであろうArray。

同じサイズの要素を並べただけのデータ構造です。
添字(index)を使うことによって瞬時にデータにアクセスすることが出来ます。
要素数が決まっているためサイズを拡張するには、新しい配列にデータのコピーをする必要があります。

array

▼計算量
先頭データのアクセス：O(1)
中間データのアクセス：O(1)
末尾データのアクセス：O(1)
先頭データの追加：不可
末尾データの追加：不可
要素が含まれているかの検索：O(n)

ベクター(Vector)

配列とほぼ同じですが、以下の様な特徴があります。

データのアクセスに関しては配列と同じだが要素数を追加したり削除したり出来ます。
ただ、要素数の追加には余分なメモリや計算が必要になってきます。

▼計算量
先頭データのアクセス：O(1)
中間データのアクセス：O(1)
末尾データのアクセス：O(1)
先頭データの追加：O(n)
末尾データの追加：O(1)
要素が含まれているかの検索：O(n)

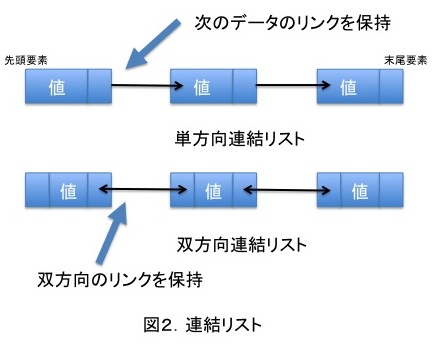
連結リスト(LinkedList)

javaではLinkedListクラスに当たります。
値の中に次のデータの格納場所(リンク、ポインタ)を持ちます。

次のデータのリンクのみを保持したものを”単方向連結リスト”
さらに前のデータのリンクも保持したものを”双方向連結リスト”と呼びます。
※javaのLinkedListは双方向連結リスト

連結リストは予め要素数を用意しなくても良いのでメモリ効率はよく
またどの部分にも高速にデータを追加することが出来ます。

しかし、要素の検索ではすべてのデータを調べる必要があるため計算量はO(n)となります。

array

▼計算量
先頭データのアクセス：O(1)
中間データのアクセス：O(N)
末尾データのアクセス：O(1)
先頭データの追加：O(1)
中間データの追加：O(1)
末尾データの追加：O(1)
要素が含まれているかの検索：O(n)
※ここでは、双方向連結リスト

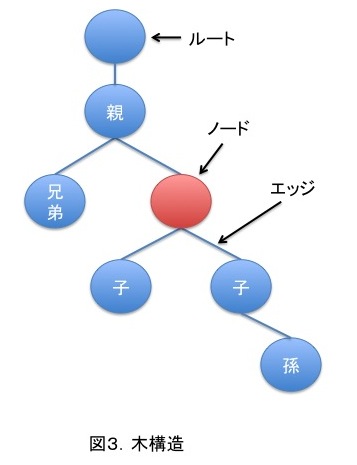
木(Tree)

ノードとエッジからなるデータ構造。

データのことをノードと呼びます。
ノードには複数の子を持つことが出来て、子ノードは１つの親ノードを持ちます。
ノード間のリンクをエッジと呼びます。
また、親がないノードを根(root)と呼びます。

言葉ではわかりづらいですが、図で表すと以下になります。
array

二分木(Binary Tree)

木構造において子を持たないノードを葉(leaf)と呼びます。
葉でないノードは最大２つの子(ノードもしくは葉)を持ちます。
２つの子は左の子、右の子と呼ばれます。

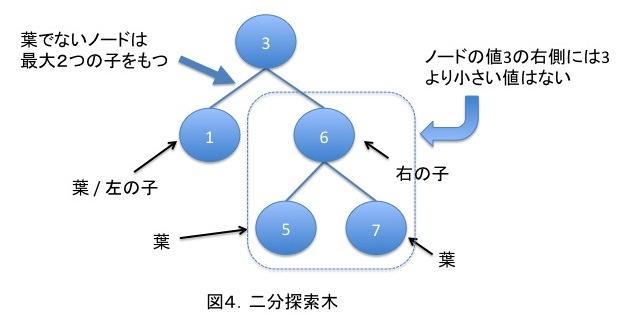
二分探索木

左の値≦自分の値≦右の値となっている二分木を二分探索木と呼びます。

二分探索木では、データ検索を高速化出来ることがあります。
図４の例では、3より小さい値を探す場合は3の右側を検索する必要がありません。
計算量は、平衡状態の場合 O(log N)となるが最悪O(N)となります。

array

二分探索木のデータ追加は入れるべきところは大方決まっています。
左の値≦自分の値≦右の値を守るため、上(ルート)からたどっていく必要があります。
計算量は検索と同じく、平衡状態の場合 O(log N)となるが最悪O(N)となります。

▼計算量
検索：O(log N)
挿入：O(log N)

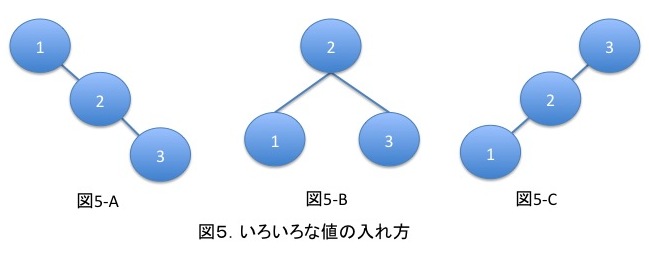
同じ値を扱うにも様々な入れ方があります。
平衡状態とは、左右のバランスが取れている状態(図5-B)のことをいいます。

array

技術記事の癖に「コードがないのは何事かっ」ということで、
最後に簡単な二分探索木を実装してみたいと思います。
(実装は開発で使っているPHPになります)

[sourcecode lang="php"]
class TreeNode {
    public $value = null;
    public $left  = null;
    public $right = null;

    public function __construct($value)
    {
        $this->value = $value;
    }
}

class Tree {
    private $root = null;
    private $count = 0;

    public function search($value)
    {
        $this->count = 0;
        $isContains = $this->_search($this->root, $value);
        echo "Count: ".$this->count." / ";
        return $isContains;
    }

    private function _search($node, $value)
    {
        $this->count++;
        if ($node === null)
            return false;

        if ($node->value === $value)
            return true;

        if ($value < $node->value) {
            // 入力よりノードの値が大きかったら左の子を見る
            return $this->_search($node->left, $value);
        } else {
            // 入力よりノードの値が小さかったら右の子を見る
            return $this->_search($node->right, $value);
        }
    }

    public function insert($value)
    {
        if ($this->root === null) {
            $this->root = new TreeNode($value);
            return;
        }
        $node = $this->root;

        while(true) {
            if ($value <= $node->value) {
                if ($node->left !== null) {
                    $node = $node->left;
                } else {
                    $node->left = new TreeNode($value);
                    return;
                }
            } else {
                if ($node->right !== null) {
                    $node = $node->right;
                } else {
                    $node->right = new TreeNode($value);
                    return;
                }
            }
        }
    }
}
[/sourcecode]

[sourcecode lang="php"]

class TreeNode {

public $value = null;

public $left = null;

public $right = null;

public function __construct($value)

{

$this->value = $value;

}

class Tree {

private $root = null;

private $count = 0;

public function search($value)

{

$this->count = 0;

$isContains = $this->_search($this->root, $value);

echo "Count: ".$this->count." / ";

return $isContains;

}

private function _search($node, $value)

{

$this->count++;

if ($node === null)

return false;

if ($node->value === $value)

return true;

if ($value < $node->value) {

// 入力よりノードの値が大きかったら左の子を見る

return $this->_search($node->left, $value);

} else {

// 入力よりノードの値が小さかったら右の子を見る

return $this->_search($node->right, $value);

}

public function insert($value)

{

if ($this->root === null) {

$this->root = new TreeNode($value);

return;

}

$node = $this->root;

while(true) {

if ($value <= $node->value) {

if ($node->left !== null) {

$node = $node->left;

} else {

$node->left = new TreeNode($value);

return;

}

} else {

if ($node->right !== null) {

$node = $node->right;

} else {

$node->right = new TreeNode($value);

return;

}

[/sourcecode]

上記の実装は平衡木になるよう作られていないため
データの入力順によって結果が変わってきます。

そこで、以下のようなケースでテストを行うと、、、

[sourcecode lang="php"]
mukku% php tree.php
Case.1 -- ツリーに1,2,3の順で追加
Search: 1 / Count: 1 / bool(true)
Search: 2 / Count: 2 / bool(true)
Search: 3 / Count: 3 / bool(true)

Case.2 -- ツリーに2,1,3の順で追加
Search: 1 / Count: 2 / bool(true)
Search: 2 / Count: 1 / bool(true)
Search: 3 / Count: 2 / bool(true)

Case.3 -- ツリーに3,2,1の順で追加
Search: 1 / Count: 3 / bool(true)
Search: 2 / Count: 2 / bool(true)
Search: 3 / Count: 1 / bool(true)

# Searchが検索した値、Countがたどった回数になります。
[/sourcecode]

[sourcecode lang="php"]

mukku% php tree.php

Case.1 -- ツリーに1,2,3の順で追加

Search: 1 / Count: 1 / bool(true)

Search: 2 / Count: 2 / bool(true)

Search: 3 / Count: 3 / bool(true)

Case.2 -- ツリーに2,1,3の順で追加

Search: 1 / Count: 2 / bool(true)

Search: 2 / Count: 1 / bool(true)

Search: 3 / Count: 2 / bool(true)

Case.3 -- ツリーに3,2,1の順で追加

Search: 1 / Count: 3 / bool(true)

Search: 2 / Count: 2 / bool(true)

Search: 3 / Count: 1 / bool(true)

# Searchが検索した値、Countがたどった回数になります。

[/sourcecode]

まさに、図５の通りの結果になりました！！(全然良くない。。。)
二分探索木の検索を有効に使うには平衡木を作る必要があるのです。

まとめ

その他のデータ構造には、スタック、キューや連想配列など、さらにはもっと複雑なものもあります。
実際、実装をはじめると慣れたデータ構造を使ってしまいがちですがデータの特性、利用されるアルゴリズムによってデータ構造を使い分けていきたいです。

ケーステストのソース

[sourcecode lang="php"]
echo "Case.1 -- ツリーに1,2,3の順で追加".PHP_EOL;
$tree1 = insertNodes(array(1, 2, 3));
searchNode($tree1, array(1, 2, 3));

echo "Case.2 -- ツリーに2,1,3の順で追加".PHP_EOL;
$tree2 = insertNodes(array(2, 1, 3));
searchNode($tree2, array(1, 2, 3));

echo "Case.3 -- ツリーに3,2,1の順で追加".PHP_EOL;
$tree3 = insertNodes(array(3, 2, 1));
searchNode($tree3, array(1, 2, 3));

function insertNodes($nodes)
{
    $tree = new Tree();
    foreach ($nodes as $node) {
        $tree->insert($node);
    }
    return $tree;
}

function searchNode($tree, $nodes)
{
    foreach ($nodes as $node) {
        echo "Search: ".$node." / ";
        var_dump($tree->search($node));
    }
    echo PHP_EOL;
}[/sourcecode]